Sliding Window Algorithm Sliding Window Algorithm Continuous 1s

Window Sliding Technique is a computational technique which aims to reduce the use of nested loop and replace it with a single loop, thereby reducing the time complexity.

What is Sliding Window?

Consider a long chain connected together. Suppose you want to apply oil in the complete chain with your hands, without pouring the oil from above.

One way to do so is to:

• pick some oil,
• apply onto a section of chain,
• then again pick some oil
• then apply it to the next section where oil is not applied yet
• and so on till the complete chain is oiled.

Another way to do so, is to use a cloth, dip it in oil, and then hold onto one end of the chain with this cloth. Then instead of re-dipping it again and again, just slide the cloth with hand onto the next section, and next, and so on till the other end.

The second way is known as the Sliding window technique and the portion which is slided from one end to end, is known as Sliding Window.

Sliding window technique

Prerequisite to use Sliding window technique

The use of Sliding Window technique can be done in a very specific scenario, where the size of window for computation is fixed throughout the complete nested loop. Only then the time complexity can be reduced.

How to use Sliding Window Technique?

The general use of Sliding window technique can be demonstrated as following:

1. Find the size of window required
2. Compute the result for 1st window, i.e. from start of data structure
3. Then use a loop to slide the window by 1, and keep computing the result window by window.

Examples to illustrate the use of Sliding window technique

Example: Given an array of integers of size 'n', Our aim is to calculate the maximum sum of 'k' consecutive elements in the array.

Input  : arr[] = {100, 200, 300, 400}, k = 2
Output : 700

Input  : arr[] = {1, 4, 2, 10, 23, 3, 1, 0, 20}, k = 4
Output : 39
We get maximum sum by adding subarray {4, 2, 10, 23} of size 4.

Input  : arr[] = {2, 3}, k = 3
Output : Invalid
There is no subarray of size 3 as size of whole array is 2.

Naive Approach: So, let's analyze the problem with Brute Force Approach. We start with first index and sum till k-th element. We do it for all possible consecutive blocks or groups of k elements. This method requires nested for loop, the outer for loop starts with the starting element of the block of k elements and the inner or the nested loop will add up till the k-th element.

Consider the below implementation :

C++

#include <bits/stdc++.h>

using namespace std;

int maxSum( int arr[], int n, int k)

{

int max_sum = INT_MIN;

for ( int i = 0; i < n - k + 1; i++) {

int current_sum = 0;

for ( int j = 0; j < k; j++)

current_sum = current_sum + arr[i + j];

max_sum = max(current_sum, max_sum);

}

return max_sum;

}

int main()

{

int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };

int k = 4;

int n = sizeof (arr) / sizeof (arr[0]);

cout << maxSum(arr, n, k);

return 0;

}

C

#include <limits.h>

#include <math.h>

#include <stdio.h>

int max( int num1, int num2)

{

return (num1 > num2) ? num1 : num2;

}

int maxSum( int arr[], int n, int k)

{

int max_sum = INT_MIN;

for ( int i = 0; i < n - k + 1; i++) {

int current_sum = 0;

for ( int j = 0; j < k; j++)

current_sum = current_sum + arr[i + j];

max_sum = max(current_sum, max_sum);

}

return max_sum;

}

int main()

{

int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };

int k = 4;

int n = sizeof (arr) / sizeof (arr[0]);

printf ( "%d" , maxSum(arr, n, k));

return 0;

}

Java

class GFG {

static int maxSum( int arr[], int n, int k)

{

int max_sum = Integer.MIN_VALUE;

for ( int i = 0 ; i < n - k + 1 ; i++) {

int current_sum = 0 ;

for ( int j = 0 ; j < k; j++)

current_sum = current_sum + arr[i + j];

max_sum = Math.max(current_sum, max_sum);

}

return max_sum;

}

public static void main(String[] args)

{

int arr[] = { 1 , 4 , 2 , 10 , 2 , 3 , 1 , 0 , 20 };

int k = 4 ;

int n = arr.length;

System.out.println(maxSum(arr, n, k));

}

}

Python3

import sys

INT_MIN = - sys.maxsize - 1

def maxSum(arr, n, k):

max_sum = INT_MIN

for i in range (n - k + 1 ):

current_sum = 0

for j in range (k):

current_sum = current_sum + arr[i + j]

max_sum = max (current_sum, max_sum)

return max_sum

arr = [ 1 , 4 , 2 , 10 , 2 ,

3 , 1 , 0 , 20 ]

k = 4

n = len (arr)

print (maxSum(arr, n, k))

C#

using System;

class GFG {

static int maxSum( int [] arr, int n, int k)

{

int max_sum = int .MinValue;

for ( int i = 0; i < n - k + 1; i++) {

int current_sum = 0;

for ( int j = 0; j < k; j++)

current_sum = current_sum + arr[i + j];

max_sum = Math.Max(current_sum, max_sum);

}

return max_sum;

}

public static void Main()

{

int [] arr = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };

int k = 4;

int n = arr.Length;

Console.WriteLine(maxSum(arr, n, k));

}

}

PHP

<?php

?>

<?php

function maxSum( $arr , $n , $k )

{

$max_sum = PHP_INT_MIN ;

for ( $i = 0; $i < $n - $k + 1; $i ++)

{

$current_sum = 0;

for ( $j = 0; $j < $k ; $j ++)

$current_sum = $current_sum +

$arr [ $i + $j ];

$max_sum = max( $current_sum , $max_sum );

}

return $max_sum ;

}

$arr = array (1, 4, 2, 10, 2, 3, 1, 0, 20);

$k = 4;

$n = count ( $arr );

echo maxSum( $arr , $n , $k );

?>

Javascript

<script>

function maxSum( arr, n, k){

let max_sum = Number.MIN_VALUE;

for (let i = 0; i < n - k + 1; i++) {

let current_sum = 0;

for (let j = 0; j < k; j++)

current_sum = current_sum + arr[i + j];

max_sum = Math.max(current_sum, max_sum);

}

return max_sum;

}

let arr = [ 1, 4, 2, 10, 2, 3, 1, 0, 20 ];

let k = 4;

let n = arr.length;

document.write(maxSum(arr, n, k));

</script>

It can be observed from the above code that the time complexity is O(k*n) as it contains two nested loops.

Sliding Window Technique: The technique can be best understood with the window pane in bus, consider a window of length n and the pane which is fixed in it of length k. Consider, initially the pane is at extreme left i.e., at 0 units from the left. Now, co-relate the window with array arr[] of size n and pane with current_sum of size k elements. Now, if we apply force on the window such that it moves a unit distance ahead. The pane will cover next k consecutive elements.

Applying sliding window technique :

1. We compute the sum of first k elements out of n terms using a linear loop and store the sum in variable window_sum.
2. Then we will graze linearly over the array till it reaches the end and simultaneously keep track of maximum sum.
3. To get the current sum of block of k elements just subtract the first element from the previous block and add the last element of the current block .

The below representation will make it clear how the window slides over the array.

Consider an array arr[] = {5, 2, -1, 0, 3} and value of k = 3 and n = 5

This is the initial phase where we have calculated the initial window sum starting from index 0 . At this stage the window sum is 6. Now, we set the maximum_sum as current_window i.e 6.

Now, we slide our window by a unit index. Therefore, now it discards 5 from the window and adds 0 to the window. Hence, we will get our new window sum by subtracting 5 and then adding 0 to it. So, our window sum now becomes 1. Now, we will compare this window sum with the maximum_sum. As it is smaller we wont the change the maximum_sum.

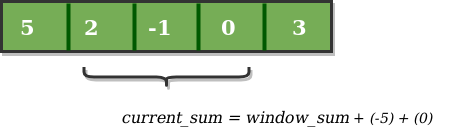
Similarly, now once again we slide our window by a unit index and obtain the new window sum to be 2. Again we check if this current window sum is greater than the maximum_sum till now. Once, again it is smaller so we don't change the maximum_sum.
Therefore, for the above array our maximum_sum is 6.

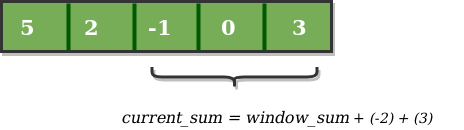
Below is the code for above approach:

C++

#include <iostream>

using namespace std;

int maxSum( int arr[], int n, int k)

{

if (n < k) {

cout << "Invalid" ;

return -1;

}

int max_sum = 0;

for ( int i = 0; i < k; i++)

max_sum += arr[i];

int window_sum = max_sum;

for ( int i = k; i < n; i++) {

window_sum += arr[i] - arr[i - k];

max_sum = max(max_sum, window_sum);

}

return max_sum;

}

int main()

{

int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };

int k = 4;

int n = sizeof (arr) / sizeof (arr[0]);

cout << maxSum(arr, n, k);

return 0;

}

Java

class GFG {

static int maxSum( int arr[], int n, int k)

{

if (n < k) {

System.out.println( "Invalid" );

return - 1 ;

}

int max_sum = 0 ;

for ( int i = 0 ; i < k; i++)

max_sum += arr[i];

int window_sum = max_sum;

for ( int i = k; i < n; i++) {

window_sum += arr[i] - arr[i - k];

max_sum = Math.max(max_sum, window_sum);

}

return max_sum;

}

public static void main(String[] args)

{

int arr[] = { 1 , 4 , 2 , 10 , 2 , 3 , 1 , 0 , 20 };

int k = 4 ;

int n = arr.length;

System.out.println(maxSum(arr, n, k));

}

}

Python3

def maxSum(arr, k):

n = len (arr)

if n < k:

print ( "Invalid" )

return - 1

window_sum = sum (arr[:k])

max_sum = window_sum

for i in range (n - k):

window_sum = window_sum - arr[i] + arr[i + k]

max_sum = max (window_sum, max_sum)

return max_sum

arr = [ 1 , 4 , 2 , 10 , 2 , 3 , 1 , 0 , 20 ]

k = 4

print (maxSum(arr, k))

C#

using System;

class GFG {

static int maxSum( int [] arr, int n, int k)

{

if (n < k) {

Console.WriteLine( "Invalid" );

return -1;

}

int max_sum = 0;

for ( int i = 0; i < k; i++)

max_sum += arr[i];

int window_sum = max_sum;

for ( int i = k; i < n; i++) {

window_sum += arr[i] - arr[i - k];

max_sum = Math.Max(max_sum, window_sum);

}

return max_sum;

}

public static void Main()

{

int [] arr = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };

int k = 4;

int n = arr.Length;

Console.WriteLine(maxSum(arr, n, k));

}

}

PHP

<?php

function maxSum( $arr , $n , $k )

{

if ( $n < $k )

{

echo "Invalid" ;

return -1;

}

$max_sum = 0;

for ( $i = 0; $i < $k ; $i ++)

$max_sum += $arr [ $i ];

$window_sum = $max_sum ;

for ( $i = $k ; $i < $n ; $i ++)

{

$window_sum += $arr [ $i ] - $arr [ $i - $k ];

$max_sum = max( $max_sum , $window_sum );

}

return $max_sum ;

}

$arr = array (1, 4, 2, 10, 2, 3, 1, 0, 20);

$k = 4;

$n = count ( $arr );

echo maxSum( $arr , $n , $k );

?>

Javascript

<script>

function maxSum(arr, n, k) {

let max = 0;

let sum = 0;

for (let i = 0; i < k; i++) {

sum += arr[i];

max = sum;

}

for (let i = k; i < n; i++) {

sum += arr[i] - arr[i - k];

if (sum > max) {

max = sum;

}

}

return max;

}

let arr = [1, 4, 2, 10, 2, 3, 1, 0, 20];

let k = 4;

let n = arr.length;

document.write(maxSum(arr, n, k));

</script>

Now, it is quite obvious that the Time Complexity is linear as we can see that only one loop runs in our code. Hence, our Time Complexity is O(n).

We can use this technique to find max/min k-subarray, XOR, product, sum, etc. Refer sliding window problems for such problems.

• Recent Articles on Window Sliding Technique
• Practice Questions on Window Sliding
• DSA Self Paced – The Most used and Trusted Course on DSA

This article is contributed by Kanika Thakral. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

martinteredly.blogspot.com

Source: https://www.geeksforgeeks.org/window-sliding-technique/